Teorie k modifikovanému sinusu

Verze pro tisk (.pdf)

Při konstrukci autobateriového měniče síťového napětí jsem se zabýval modifikovaným sinusovým signálem. U modifikovaného sinusového síťového napětí platí, že frekvence signálu odpovídá 50 Hz, amplituda napětí je 326 V a celkové efektivní napětí je 230 V. Porovnání průběhu modifikovaného sinusu a klasického sinusového síťového napětí je na obrázku 1. Konkrétně jsem se zamýšlel nad tím, jak dlouhé musí být pulzy T₁/2. Jedna z věcí, kterou mi dalo studium na vysoké škole je pocit, že vzorečku, který neumím odvodit, tak úplně nevěřím. Proto jsem se hlouběji nad tímto problémem zamyslel. A vy můžete taky, bude ovšem potřeba mít alespoň základní znalosti pokročilejší matematiky, konkrétně integrálního počtu.

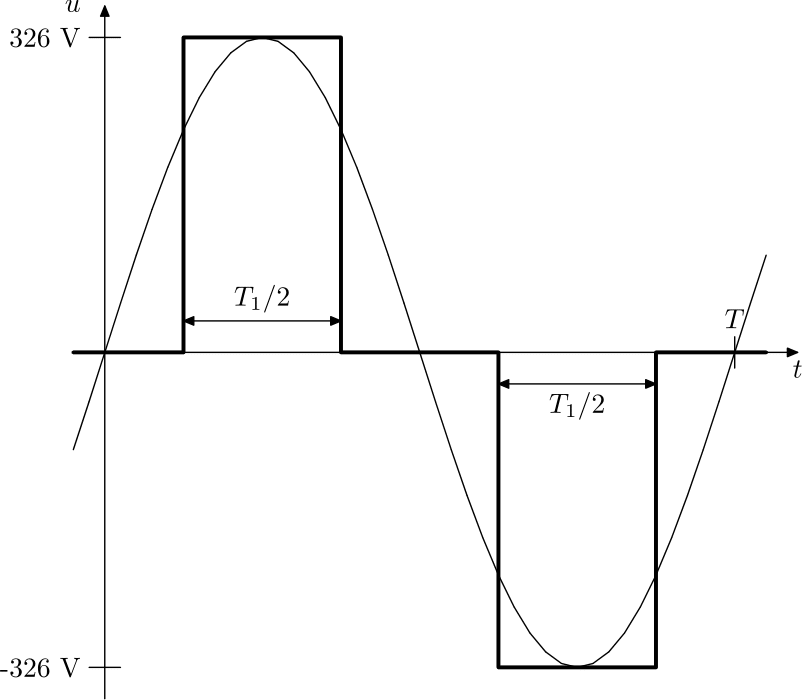
Obrazek 1: Porovnání průběhu síťového napětí a modifikovaného sinusu.

Začněme tedy otázkou, co je to efektivní napětí. Mějme zdroj střídavého napětí u(t) s periodou T a zdroj stejnosměrného napětí U_eff. Na oba zdroje připojíme rezistory se stejným odporem R. Aby stejnosměrné napětí U_eff bylo efektivní napětím, musí platit, že práce, která se vykoná na obou rezistorech za periodu T je stejná. Neboli musí platit:

$\begin{displaymath} \int_{0}^{T} \frac{U^2_{eff}}{R}\mathrm{d}t = \int_{0}^{T} \frac{u^2(t)}{R}\mathrm{d}t\,. \end{displaymath}$

Vycházíme z toho, že práce W = ∫₀^T P(t)dt, kde P(t) je okamžitý výkon, pro který platí P(t)=u(t)· i(t)=u²(t)/R.

Výše uvedený vztah můžeme dále upravovat

$\begin{displaymath} \frac{1}{R}U^2_{eff}\int_{0}^{T} \mathrm{d}t = \frac{1}{R}\int_{0}^{T} u^2(t)\mathrm{d}t \end{displaymath}$

$\begin{displaymath} U^2_{eff}T = \int_{0}^{T} u^2(t)\mathrm{d}t \end{displaymath}$

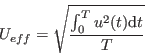
$\begin{displaymath} U_{eff} = \sqrt{\frac{\int_{0}^{T} u^2(t)\mathrm{d}t}{T}} \end{displaymath}$

Pro sinusový průběh napětí u(t)=Asin(2π t / T), kde A je amplituda signálu, platí

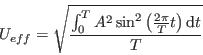
$\begin{displaymath} U_{eff} = \sqrt{\frac{\int_{0}^{T} A^2 \sin^2\left( \frac{2 \pi}{T} t\right)\mathrm{d}t}{T}} \end{displaymath}$

použijeme substituci z=2 π / T t, d z = T / (2 π)d t a tedy dále upravíme

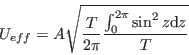
$\begin{displaymath} U_{eff} = A \sqrt{\frac{T}{2 \pi }\frac{\int_{0}^{2 \pi} \sin^2 z\mathrm{d}z}{T}} \end{displaymath}$

Výpočet

$\begin{displaymath} \int_{0}^{2 \pi} \sin^2 z\mathrm{d}z = \pi \end{displaymath}$

můžeme najít v tabulkách, nicméně dá se to celkem elegantně spočítat, proto jsem výpočet dal pro zajímavost na konec tohoto textu.

Dosadíme do vztahu

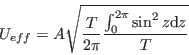
$\begin{displaymath} U_{eff} = A \sqrt{\frac{T}{2 \pi }\frac{\int_{0}^{2 \pi} \sin^2 z\mathrm{d}z}{T}} \end{displaymath}$

a dostaneme

$\begin{displaymath} U_{eff} = A \sqrt{\frac{T}{2 \pi }\frac{\pi}{T}} = A \sqrt{\frac{1}{2}} \end{displaymath}$

Což je známý vztah pro sinusový signál A = √2 U_eff.

U modifikovaného sinusu víme, že část periody T₂=T−T₁ je signál nulový a část periody T₁ je signál roven amplitudě A (resp. amplitudě −A). Vztah

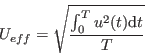
$\begin{displaymath} U_{eff} = \sqrt{\frac{\int_{0}^{T} u^2(t)\mathrm{d}t}{T}} \end{displaymath}$

tak můžeme pro modifikovaný sinus upravit

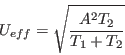
$\begin{displaymath} U_{eff} = \sqrt{\frac{A^2 T_2}{T_1 + T_2}} \end{displaymath}$

Snadno nahlédneme, že pokud T₁ = T₂ = T/2, tak

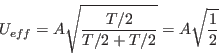
$\begin{displaymath} U_{eff} = A \sqrt{\frac{T/2}{T/2 + T/2}} = A \sqrt{\frac{1}{2}} \end{displaymath}$

a modifikovaný sinus tak bude mít pro danou amplitudu stejné efektivní napětí, jako sinusový signál.

Výpočet

$\begin{displaymath} \int_{0}^{2 \pi} \sin^2 z\mathrm{d}z = \pi \end{displaymath}$

není úplně snadný, ale dá se využít následující trik s výpočtem integrálu pomocí metody per-partes (∫u(x) v′(x) (d)x = u(x) v(x) − ∫u′(x) v(x) (d)x), kdy u=sin(z), v′=sin(z) a tedy u′=cos(z), v=−cos(z)

$\begin{displaymath} \int_{0}^{2 \pi} \sin^2 z\mathrm{d}z = \left[ \sin(z) \cos (... ...0}^{z=2\pi} - \int_{0}^{2 \pi} \cos (z) (-\cos(z)) \mathrm{d}z \end{displaymath}$

výraz [ sin(z) cos(z) ]_z=0^z=2π je roven nule a zároveň platí, že cos²(z) = 1 − sin²(z), tedy

$\begin{displaymath} \int_{0}^{2 \pi} \sin^2 z\mathrm{d}z = \int_{0}^{2 \pi} [1 -... ...}^{2 \pi} \mathrm{d}z - \int_{0}^{2 \pi} \sin^2(x) \mathrm{d}z \end{displaymath}$

Na vztah se můžeme podívat jako na rovnici a − ∫₀^{2 π} sin²(x) dz přehodit doleva.

$\begin{displaymath} 2 \int_{0}^{2 \pi} \sin^2 z\mathrm{d}z = \int_{0}^{2 \pi} [1 - \sin^2(x)] \mathrm{d}z = [z]_{z=0}^{z=2 \pi} = 2 \pi \end{displaymath}$

a konečně

$\begin{displaymath} \int_{0}^{2 \pi} \sin^2 z\mathrm{d}z = \pi \end{displaymath}$